デジタルフィルタ(IIRフィルタ)において、マイコンの実装方法とその意味について説明します。
特に一次のIIRフィルタとアナログ電子回路との関係を深掘りします。
本記事は マイコン等で実現するデジタルフィルタの実装例とアナログフィルタとの関係を説明します。
■ デジタルフィルタとは
本記事では IIRフィルタについて重点的に見ていきますが、基本のデジタルフィルタとは何か から簡単に説明します。
FIRフィルタとIIRフィルタ
デジタルフィルタには FIRフィルタ と IIRフィルタ の二種類があります。
細かい説明は 他の記事に譲りますが、“FIRフィルタ(Finite Impulse Response)はシンプルで安定“、“IIRフィルタ(Infinite Impulse Response)はFIRフィルタに比べ レジスタ数(メモリ数)を削減でき性能高い。ただし、パラメータ設定によっては不安定になる“ など、両者にはそれぞれの特徴があります。
| FIRフィルタ | IIRフィルタ | |
| 呼び名 | Finite Impulse Response (有限インパルス応答) | Infinite Impulse Response (無限インパルス応答) |
| 特徴 | 移動平均もFIRフィルタに相当する。 常に安定である。 | 極と零点を組み合わせる。 少ないメモリと演算量で実装できる。 |
| デメリット | 群遅延が発生する。 | 設計によっては発振する。 |
ブロック線図と伝達関数
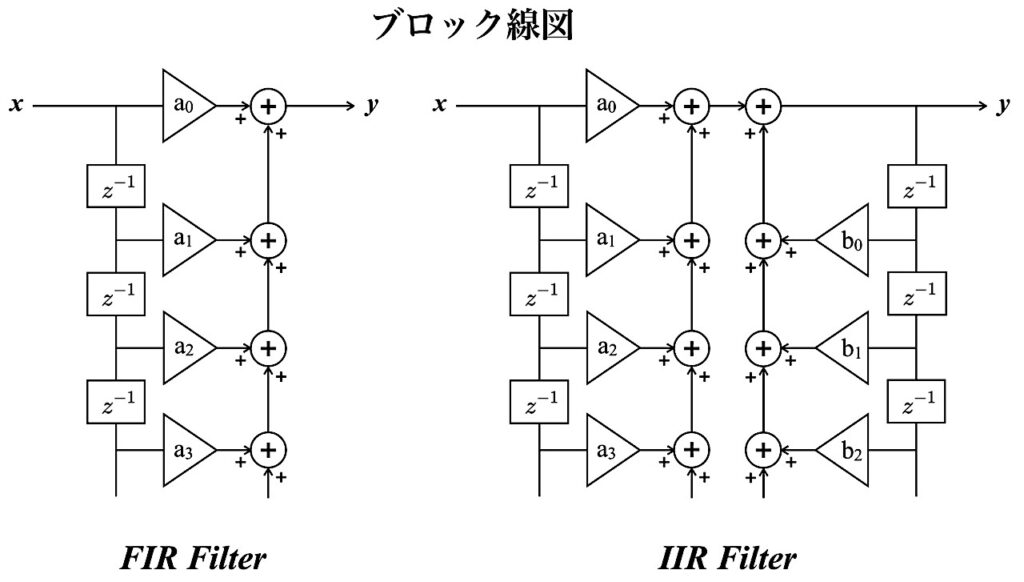
これもよくあるブロック線図です。
ブロック線図から分かるIIRフィルタの特性は、出力項を含めて計算するので パラメータの設定次第で 系が不安定になる(出力が発振してしまう)特性がみてとれます。反対にFIRフィルタには出力項を含めて計算することがないため、常に安定になることがわかります。
FIRフィルタの伝達関数は
$$ H(z) = a_0+a_1・z^{-1}+a_2・z^{-2}+a_3・z^{-3}+・・・ $$
IIRフィルタの伝達関数は
$$ H(z) = \frac{a_0+a_1・z^{-1}+a_2・z^{-2}+a_3・z^{-3}+・・・}{1-b_0・z^{-1}-b_1・z^{-2}-b_2・z^{-3}-・・・} $$
ここでは、FIRフィルタとIIRフィルタの伝達関数の形を確認してもらいたいです。
IIRフィルタの伝達関数は 分数になっており 分子分母にzがあるので、極と零点をとることが分かります。
■ プログラム上の実装方法
基本を説明した後 早速ですが、マイコン上(C言語)でどう実装するかを説明します。本記事では、マイコン上での話をしているが DSPなどのアセンブラ言語でも利用できます。
今回は一次IIRフィルタの実装(ローパスフィルタ)を例にします。
マイコンへの実装例
デジタルフィルタの実装は、簡単な記載で 実装できます。
//parameters
float alpha = 0.5; // 0 < alpha < 1
float x; //Input
float y; //Output
//IIR Filter
int IIR_Filter(int x){
static int y_old;
y = alpha * y_old + (1 - alpha) * x
y_old = y;
return y;
}x は 入力、y は 出力、αは フィルタの係数である。※αの詳細は以下の記事で明らかにする。
計算式は $ y(n) = α・y(n-1) + (1-α)・x(n) $ だけ です。
デジタルフィルタの構成は、「デジタルフィルタの計算式」と 「次回の計算に必要な値の保持」になります。
保持する値は staticなど 静的に保存場所を確保して 代入する。
使い方としては、周期的に行なっている処理に 関数IIR_Fillterを呼び出せば良いです。
#include IIR_Filter.h
void main(void){
int data;
while(1){
data = getData(); //センサーからのデータを取得してdataに代入。
processed_data = IIR_Filter(data);
//以降で processed_data を利用する。
}
}例では、センサー等で得られた 何かしらのデータを変数dataに渡し、dataは IIRフィルタ処理されprocessed_data に代入される。
processed_dataはフィルタ後のデータなのでノイズの少ないデータで、後の処理を実行できます。
IIRフィルタの効果確認
IIRフィルタの効果を確認してみます。
先ほどの一次IIRフィルタ(α=0.7)をかけたときのシミュレーションをしてみます。
入力する波形(模擬波形)を下記のように設定して、IIRフィルタにかけます。
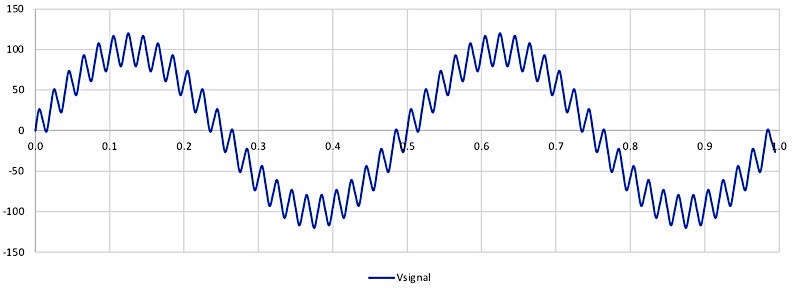
模擬波形$V_{signal}$は $V_{signal}=A_1sin(2π・f_1・t)+A_2sin(2π・f_2・t)$ 。
※信号:振幅$A_1=100$、周波数$f_1=2Hz$
ノイズ:振幅$A_2=20$、周波数$f_2=50Hz$。
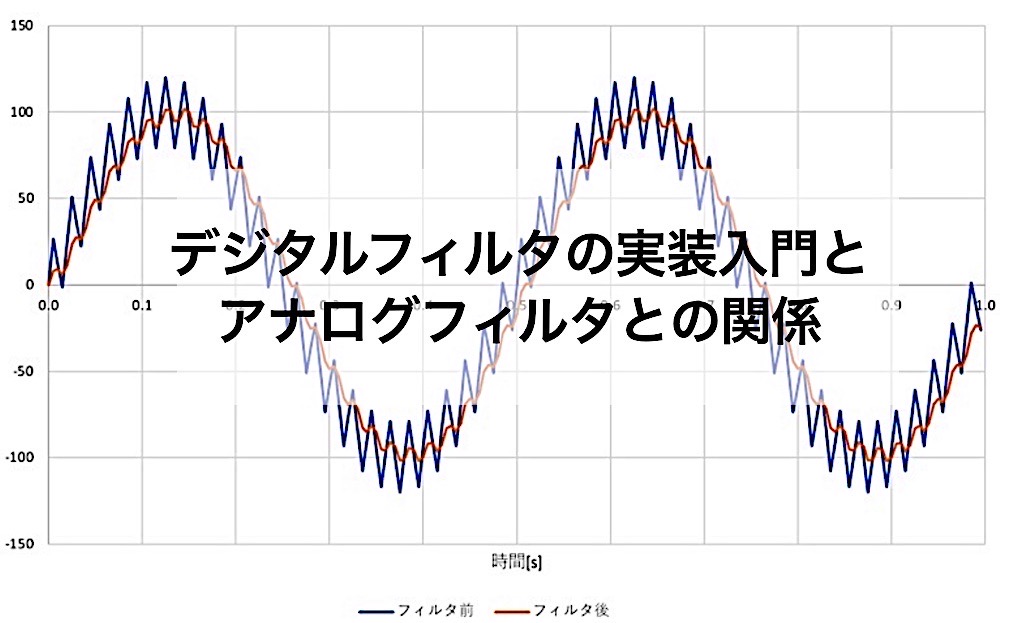
模擬波形には二つの周波数を含んだ信号波形を用意しました。低周波(2Hz)の信号を本来得たい信号波形と想定し、そこに高周波(50Hz)のノイズが重畳した波形が今回の模擬波形になります。
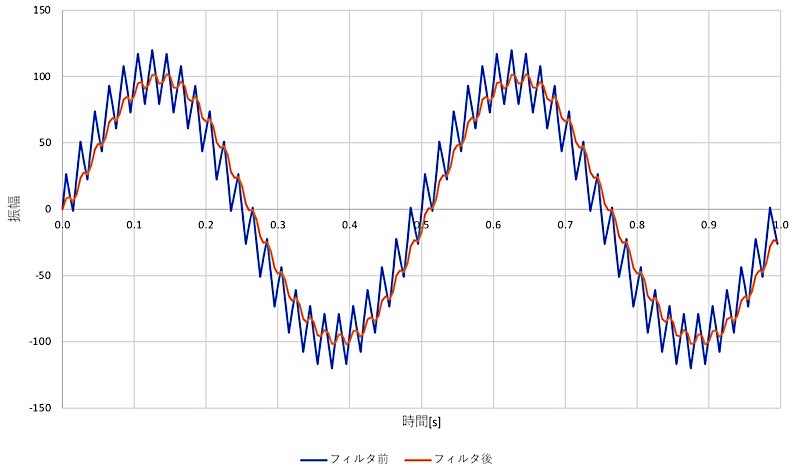
フィルター結果は以下のようになりました。

IIRフィルタによって高周波成分がカットされ、低周波成分の信号のみをうまく取り出せていることがわかります。
IIRフィルタの効果が確認できたところで、フィルタ特性を解析してみます。
■ デジタルフィルタの特性解析
今回のマイコンの実装例である1次のIIRフィルタについて 設計されたデジタルフィルタの特性を調べてみます。
伝達関数の導出
今回の実装式を再掲します。
$$ y(n) = α・y(n-1) + (1-α)・x(n) $$
z を用いて表現すると
$$ y = α・y・z^{-1}+ (1-α)・x$$
伝達関数H(z)は y/x なので
$$ H(z) = \frac{1-α}{1-α・z^{-1}} $$
以上より IIRフィルタの伝達関数が求まりました。
ゲイン特性
伝達関数H(z)を導出できたら、$z^{-1} = e^{-jθ}$とおき、$θ$に関する伝達関数G(θ)の絶対値を求めます。
$$ |G(θ)|= \frac{1-α}{\sqrt{1+α^2-2α・ \cosθ}}$$
この式より、伝達関数のゲイン特性が描けます。
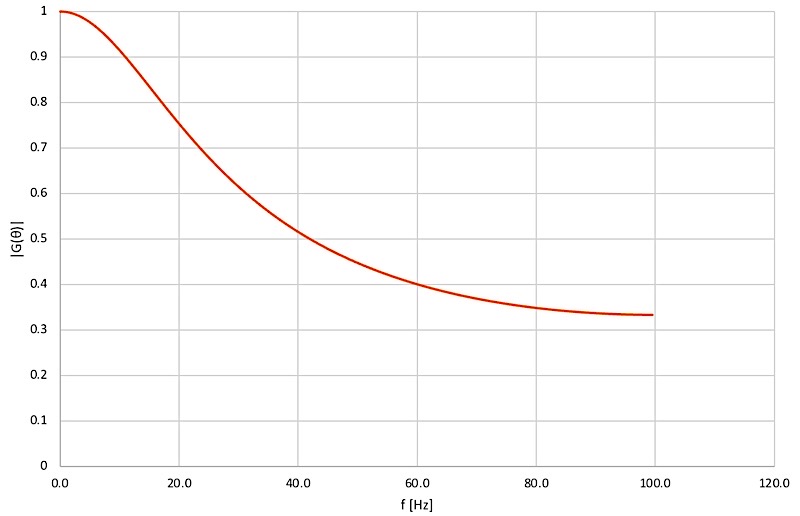
上図は α=0.5 のときの |G(θ)|のグラフになります。(サンプリング周波数 $f_s$は 200Hz とした。)
伝達関数の文字については、慣習に習い、zに関する伝達関数はHとし、θに関する伝達関数はGとしました。
カットオフ周波数$f_c$を求めるには ゲインG(θ)が 1/2 になる周波数を求めると
$ f_c = \frac{ f_s}{2π}cos^{-1}\left\{4-\frac{3}{2}(α+\frac{1}{α})\right\} $ と計算できます。
α=0.5のときのカットオフ周波数$f_c$は
$$ f_c = \frac{ 200}{2π}cos^{-1}\left\{4-\frac{3}{2}(0.5+\frac{1}{0.5})\right\} \approx 42.0[Hz] $$
上図のゲイン特性グラフからも ゲイン0.5になる周波数は42Hzあたりであることがわかり、計算が正しいことが分かります。
“ゲイン特性”と”α”の関係
αを変化させることでフィルタのゲイン特性が変化します。αを変化させてみます。
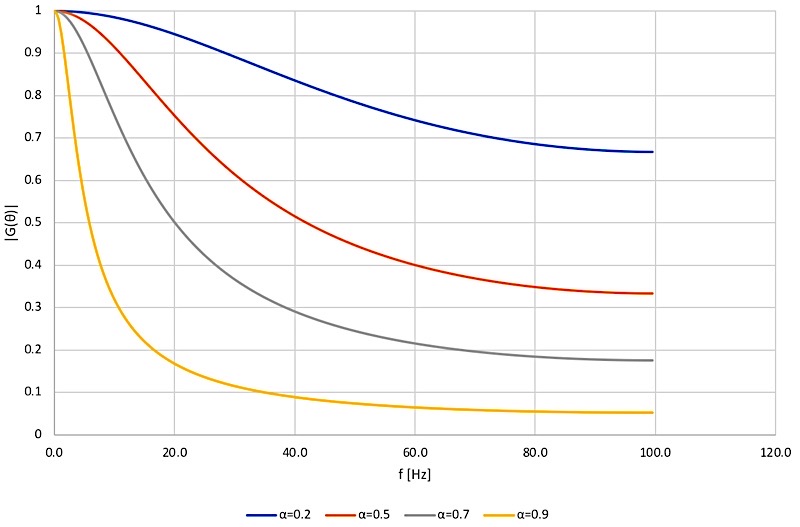
図を見て 下記が理解できると思います。
- αを大きくすると 入力は反映されづらくなり、低域成分のみ通過するフィルターになる。
- αを小さくすると 入力がそのまま反映され、高域も通過できやすくなる。
信号2Hzに対しては 約91%通過し ほぼ減衰無し。
ノイズ50Hzに対しては 約24.5%通過となり 振幅が1/4となるはずである。
(※サンプリング周波数 200Hz とした。)
■ 電子回路における意味
デジタルフィルタを アナログのフィルタ(電子回路)に落とし込む とどう考えられるか、深掘りしてみましょう。
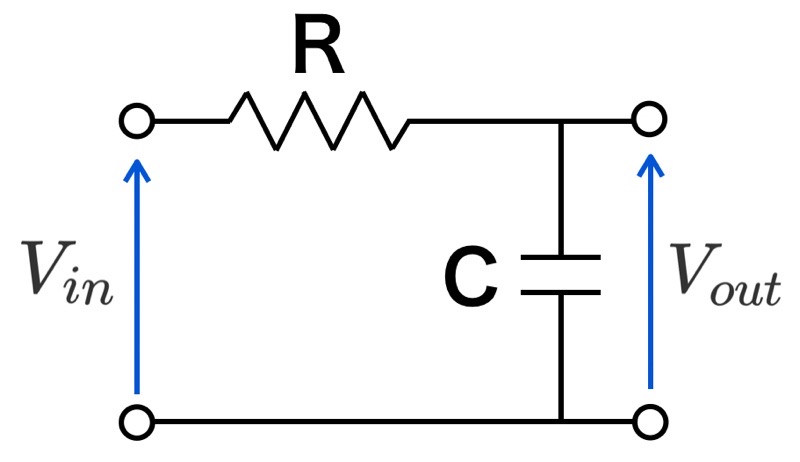
本記事で説明した1次のIIRフィルタは アナログフィルタのRCフィルタと 特性が同等だと知られています。
※正確には RCローパスフィルタの伝達関数を 後退差分のz変換すると 1次IIRフィルタと一致する。
RCローパスフィルタの伝達関数
RCのローパスフィルタを 考えます。

RCローパスフィルタの伝達関数G を求めると 入出力関係から
$$ G(jω) = \frac{V_{out}}{V_{in}} = \frac{\frac{1}{jωC}}{R+\frac{1}{jωC}}$$
$ G(jω) = \frac{1}{1+jωRC} $ と 求まります。
$ s = jω $ を利用して 伝達関数は $ G(s) = \frac{1}{1+sRC} $ と表現できます。
ここまでは 見慣れている方も多いと思います。
ここからデジタルに置き換えるため、後退差分によるz変換 $ s = \frac{1-z^{-1}}{T} $ を利用して
\begin{align} G(z) &= \frac{1}{1+\frac{1-z^{-1}}{T}RC} \\\\ &= \frac{\frac{T}{RC}}{\frac{T}{RC}+1-z^{-1}} \\\\ &= \frac{\frac{T}{RC}}{\frac{T+RC}{RC}-z^{-1}} \\\\ &= \frac{\frac{T}{T+RC}}{1-\frac{RC}{T+RC}z^{-1}} \end{align}
$ α = \frac{RC}{T+RC} $ とおくと
$$ G(z) = \frac{1-α}{1-α・z^{-1}} $$
以上のように伝達関数が IIRフィルタのものと同じになります。
つまり、一次IIRフィルタのαは アナログRCフィルタの$\frac{RC}{T+RC}$ に相当することがわかりました。
■ まとめ
本記事の要点をまとめます。
一次IIRフィルタは アナログ電子回路のRCローパスフィルタと比較できることが知られており、一通りの説明しました。
今回のIIRフィルタの対応表を示します。
| デジタル | アナログ | |
| 実装 | 一次IIRフィルタ | RCローパスフィルタ |
| パラメータ | α (0<α<1) | $\frac{RC}{T+RC}$ T(サンプリング周波数の逆数) と 時定数 RC |
| 伝達関数 | $\frac{1-α}{1-αz^{-1}}$ | $\frac{1-\frac{RC}{T+RC}}{1-\frac{RC}{T+RC}z^{-1}}$ |
アナログ回路とデジタルフィルタとの対応を理解いただけたら幸いです。
参考記事や動画
- Youtube「IIR Filters – Theory and Implementation – Phill’s Lab #32」 https://youtu.be/QRMe02kzVkA
- ブログ記事「アナログ視点で理解するデジタルフィルタ」 https://tech-blog.cerevo.com/archives/10159/



コメント